Bayesian Inference for Spatial-Temporal Non-Gaussian Data Using Predictive Stacking
arXiv preprint, 2024
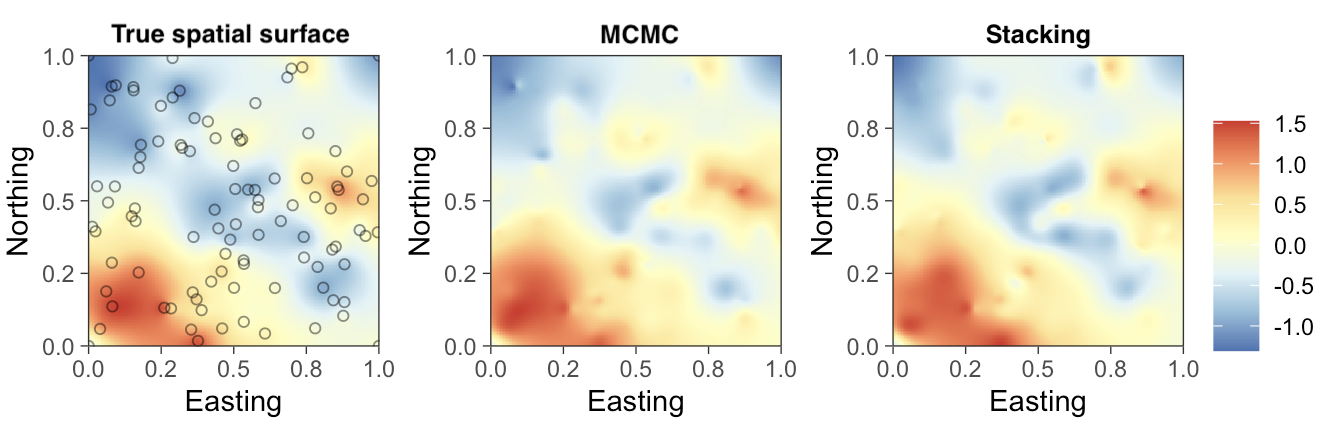
Analysing non-Gaussian spatial-temporal data typically requires introducing spatial dependence in generalised linear models through the link function of an exponential family distribution. However, unlike in Gaussian likelihoods, inference is considerably encumbered by the inability to analytically integrate out the random effects and reduce the dimension of the parameter space. Iterative estimation algorithms struggle to converge due to the presence of weakly identified parameters. We devise an approach that obviates these issues by exploiting generalised conjugate multivariate distribution theory for exponential families, which enables exact sampling from analytically available posterior distributions conditional upon some fixed process parameters. More specifically, we expand upon the Diaconis-Ylvisaker family of conjugate priors to achieve analytically tractable posterior inference for spatially-temporally varying regression models conditional on some kernel parameters. Subsequently, we assimilate inference from these individual posterior distributions over a range of values of these parameters using Bayesian predictive stacking. We evaluate inferential performance on simulated data, compare with fully Bayesian inference using Markov chain Monte Carlo and apply our proposed method to analyse spatially-temporally referenced avian count data from the North American Breeding Bird Survey database.
Recommended citation:
Pan, S., Zhang, L., Bradley, J. R., & Banerjee, S. (2024). "Bayesian inference for spatial-temporal non-Gaussian data using predictive stacking." arXiv:stat.ME.
Download Citation | DOI
