Skip to contents

Spatial Regression Models

Source: vignettes/spatial.Rmd
spatial.Rmd

In this article, we discuss the following functions -

These functions can be used to fit Gaussian and non-Gaussian spatial point-referenced data.

set.seed(1729)

Bayesian Gaussian spatial regression models

In this section, we thoroughly illustrate our method on synthetic Gaussian as well as non-Gaussian spatial data and provide code to analyze the output of our functions. We start by loading the package.

Some synthetic spatial data are lazy-loaded which includes synthetic spatial Gaussian data simGaussian, Poisson data simPoisson, binomial data simBinom and binary data simBinary. One can use the function sim_spData() to simulate spatial data. We will be applying our functions on these datasets.

Using fixed hyperparameters

We first load the data simGaussian and set up the priors. Supplying the priors is optional. See the documentation of spLMexact() to learn more about the default priors. Besides, setting the priors, we also fix the values of the spatial process parameters (spatial decay ϕ\phi and smoothness ν\nu) and the noise-to-spatial variance ratio (δ2\delta^2).

data("simGaussian")
dat <- simGaussian[1:200, ] # work with first 200 rows

muBeta <- c(0, 0)
VBeta <- cbind(c(1E4, 0.0), c(0.0, 1E4))
sigmaSqIGa <- 2
sigmaSqIGb <- 2
phi0 <- 3
nu0 <- 0.5
noise_sp_ratio <- 0.8
prior_list <- list(beta.norm = list(muBeta, VBeta),
                   sigma.sq.ig = c(sigmaSqIGa, sigmaSqIGb))
nSamples <- 1000

We define the spatial model using a formula, similar to that in the widely used lm() function in the stats package. Here, the formula y ~ x1 corresponds to the spatial linear model y(s)=β0+β1x1(s)+z(s)+ϵ(s),y(s) = \beta_0 + \beta_1 x_1(s) + z(s) + \epsilon(s)\;, where the y corresponds to the response variable y(s)y(s), which is regressed on the predictor x1 given by x1(s)x_1(s). The intercept is automatically considered within the model, and hence y ~ x1 is functionally equivalent to y ~ 1 + x1. Moreover, a spatial random effect is inherent in the model, where the spatial correlation matrix is governed by the spatial correlation function specified by the argument cor.fn. Supported correlation functions are "exponential" and "matern". The exponential covariogram is specified by the hyperparameter ϕ\phi and the Matern covariogram is specified by the hyperparameters ϕ\phi and ν\nu. Fixed values of these hyperparameters are supplied through the argument spParams. In addition, the noise-to-spatial variance ration is also fixed through the argument noise_sp_ratio.

If interested in calculation of leave-one-out predictive densities (LOO-PD), loopd must be set TRUE (the default is FALSE). Method of LOO-PD calculation can be also set by the option loopd.method which support the keywords "exact" and "psis". The option "exact" exploits the analytically available expressions of the predictive density and implements an efficient row-deletion Cholesky factor update for fast calculation and avoids refitting the model nn times, where nn is the sample size. On the other hand, "psis" implements Pareto-smoothed importance sampling and finds approximate LOO-PD and is much faster than "exact".

We pass these arguments into the function spLMexact().

mod1 <- spLMexact(y ~ x1, data = dat,
                  coords = as.matrix(dat[, c("s1", "s2")]),
                  cor.fn = "matern",
                  priors = prior_list,
                  spParams = list(phi = phi0, nu = nu0),
                  noise_sp_ratio = noise_sp_ratio, n.samples = nSamples,
                  loopd = TRUE, loopd.method = "exact",
                  verbose = TRUE)
#> ----------------------------------------
#>  Model description
#> ----------------------------------------
#> Model fit with 200 observations.
#> 
#> Number of covariates 2 (including intercept).
#> 
#> Using the matern spatial correlation function.
#> 
#> Priors:
#>  beta: Gaussian
#>  mu: 0.00    0.00    
#>  cov:
#>   10000.00    0.00   
#>   0.00    10000.00   
#> 
#>  sigma.sq: Inverse-Gamma
#>  shape = 2.00, scale = 2.00.
#> 
#> Spatial process parameters:
#>  phi = 3.00, and, nu = 0.50.
#> Noise-to-spatial variance ratio = 0.80.
#> 
#> Number of posterior samples = 1000.
#> 
#> LOO-PD calculation method = exact.
#> ----------------------------------------

Next, we can summarize the posterior samples of the fixed effects as follows.

post_beta <- mod1$samples$beta
summary_beta <- t(apply(post_beta, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
rownames(summary_beta) <- mod1$X.names
print(summary_beta)
#>                 2.5%      50%    97.5%
#> (Intercept) 1.688957 2.284946 2.955524
#> x1          4.866534 4.954401 5.040862

Leave-one-out predictive densities using PSIS

Out of curiosity, we find the LOO-PD for the same model using the approximate method that uses Pareto-smoothed importance sampling, or PSIS. See Vehtari, Gelman, and Gabry (2017) for details.

mod2 <- spLMexact(y ~ x1, data = dat,
                  coords = as.matrix(dat[, c("s1", "s2")]),
                  cor.fn = "matern",
                  priors = prior_list,
                  spParams = list(phi = phi0, nu = nu0),
                  noise_sp_ratio = noise_sp_ratio, n.samples = nSamples,
                  loopd = TRUE, loopd.method = "PSIS",
                  verbose = FALSE)

Subsquently, we compare the LOO-PD obtained by the two methods.

loopd_exact <- mod1$loopd
loopd_psis <- mod2$loopd
loopd_df <- data.frame(exact = loopd_exact, psis = loopd_psis)

library(ggplot2)
plot1 <- ggplot(data = loopd_df, aes(x = exact)) +
  geom_point(aes(y = psis), size = 1, alpha = 0.5) +
  geom_abline(slope = 1, intercept = 0, color = "red", alpha = 0.5) +
  xlab("Exact") + ylab("PSIS") + theme_bw() +
  theme(panel.background = element_blank(), 
        panel.grid = element_blank(), aspect.ratio = 1)
plot1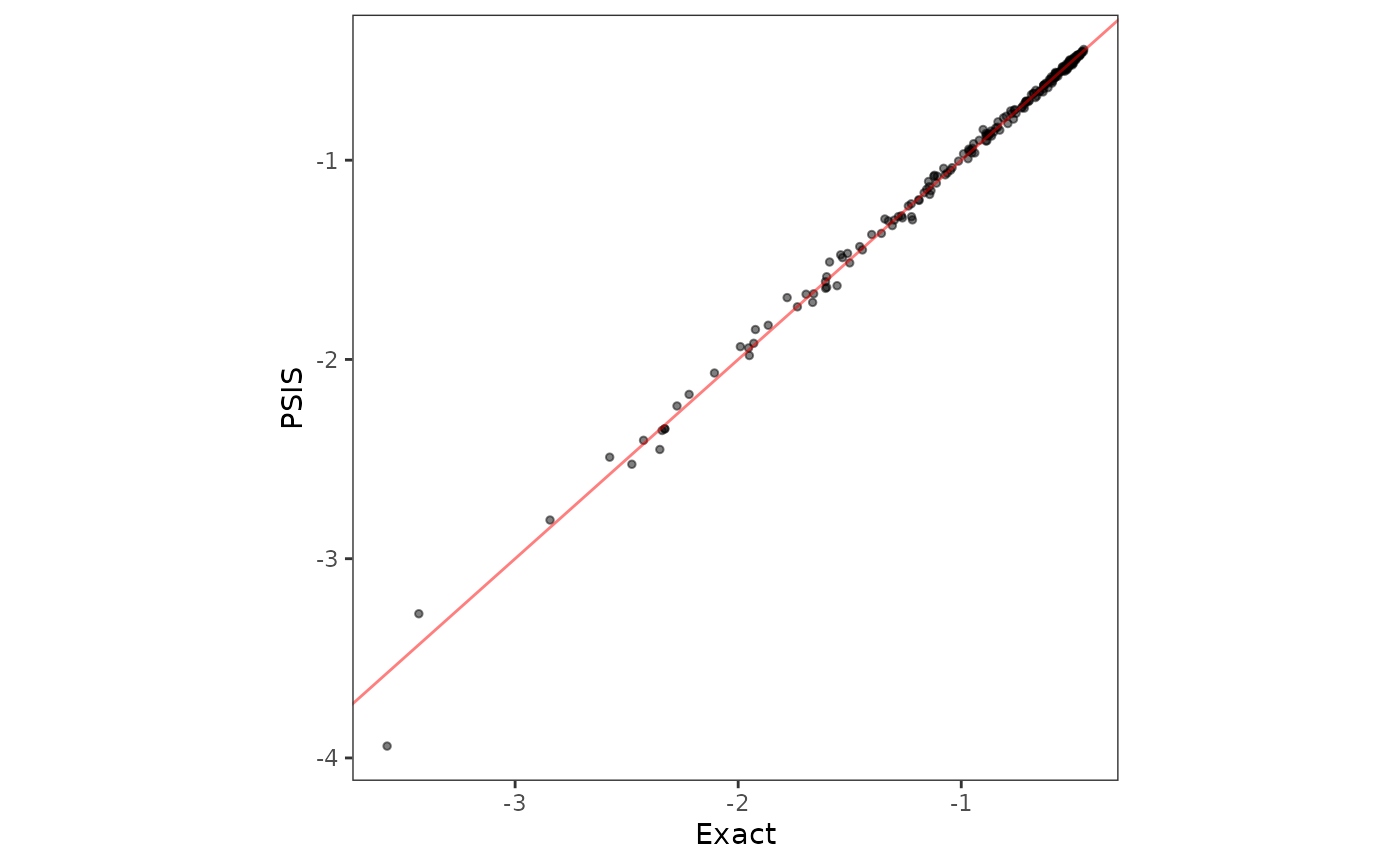

Using predictive stacking

Next, we move on to the Bayesian spatial stacking algorithm for Gaussian data. We supply the same prior list and provide some candidate values of spatial process parameters and noise-to-spatial variance ratio.

mod3 <- spLMstack(y ~ x1, data = dat,
                  coords = as.matrix(dat[, c("s1", "s2")]),
                  cor.fn = "matern",
                  priors = prior_list,
                  params.list = list(phi = c(1.5, 3, 5),
                                     nu = c(0.5, 1, 1.5),
                                     noise_sp_ratio = c(0.5, 1.5)),
                  n.samples = 1000, loopd.method = "exact",
                  parallel = FALSE, solver = "ECOS", verbose = TRUE)
#> 
#> STACKING WEIGHTS:
#> 
#>            | phi | nu  | noise_sp_ratio | weight |
#> +----------+-----+-----+----------------+--------+
#> | Model 1  |  1.5|  0.5|             0.5| 0.000  |
#> | Model 2  |  3.0|  0.5|             0.5| 0.000  |
#> | Model 3  |  5.0|  0.5|             0.5| 0.000  |
#> | Model 4  |  1.5|  1.0|             0.5| 0.242  |
#> | Model 5  |  3.0|  1.0|             0.5| 0.000  |
#> | Model 6  |  5.0|  1.0|             0.5| 0.751  |
#> | Model 7  |  1.5|  1.5|             0.5| 0.000  |
#> | Model 8  |  3.0|  1.5|             0.5| 0.000  |
#> | Model 9  |  5.0|  1.5|             0.5| 0.000  |
#> | Model 10 |  1.5|  0.5|             1.5| 0.000  |
#> | Model 11 |  3.0|  0.5|             1.5| 0.000  |
#> | Model 12 |  5.0|  0.5|             1.5| 0.000  |
#> | Model 13 |  1.5|  1.0|             1.5| 0.000  |
#> | Model 14 |  3.0|  1.0|             1.5| 0.000  |
#> | Model 15 |  5.0|  1.0|             1.5| 0.006  |
#> | Model 16 |  1.5|  1.5|             1.5| 0.000  |
#> | Model 17 |  3.0|  1.5|             1.5| 0.000  |
#> | Model 18 |  5.0|  1.5|             1.5| 0.000  |
#> +----------+-----+-----+----------------+--------+

The user can check the solver status and runtime by issuing the following.

print(mod3$solver.status)
#> [1] "optimal"
print(mod3$run.time)
#>    user  system elapsed 
#>   2.364   2.759   1.641

Analyzing samples from the stacked posterior

To sample from the stacked posterior, the package provides a helper function called stackedSampler(). Subsequent inference proceeds from these samples obtained from the stacked posterior.

post_samps <- stackedSampler(mod3)

We then collect the samples of the fixed effects and summarize them as follows.

post_beta <- post_samps$beta
summary_beta <- t(apply(post_beta, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
rownames(summary_beta) <- mod3$X.names
print(summary_beta)
#>                 2.5%      50%    97.5%
#> (Intercept) 1.032605 2.215743 3.115782
#> x1          4.871351 4.949397 5.029925

The synthetic data simGaussian was simulated using the true value β=(2,5)⊤\beta = (2, 5)^{ \scriptstyle \top }. We notice that the stacked posterior is concentrated around the truth.

library(tidyr)
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union

post_beta_df <- as.data.frame(post_beta)
post_beta_df <- post_beta_df %>%
  mutate(row = paste0("beta", row_number()-1)) %>%
  pivot_longer(-row, names_to = "sample", values_to = "value")

# True values of beta0 and beta1
truth <- data.frame(row = c("beta0", "beta1"), true_value = c(2, 5))

ggplot(post_beta_df, aes(x = value)) +
  geom_density(fill = "lightblue", alpha = 0.6) +
  geom_vline(data = truth, aes(xintercept = true_value), 
             color = "red", linetype = "dashed", linewidth = 0.5) +
  facet_wrap(~ row, scales = "free") + labs(x = "", y = "Density") +
  theme_bw() + theme(panel.background = element_blank(), 
                     panel.grid = element_blank(), aspect.ratio = 1)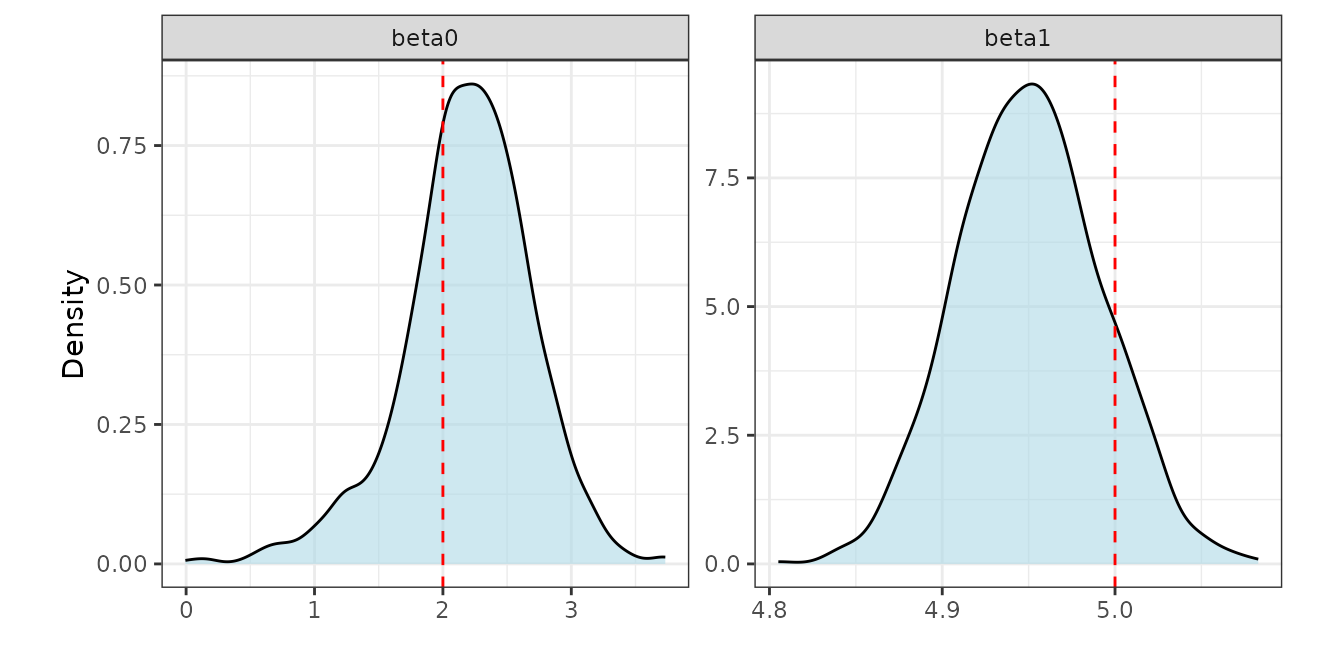

Posterior distributions of the fixed effects

Furthermore, we compare the posterior samples of the spatial random effects with their corresponding true values.

post_z <- post_samps$z
post_z_summ <- t(apply(post_z, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
z_combn <- data.frame(z = dat$z_true, zL = post_z_summ[, 1],
                      zM = post_z_summ[, 2], zU = post_z_summ[, 3])

plotz <- ggplot(data = z_combn, aes(x = z)) +
  geom_point(aes(y = zM), size = 0.75, color = "darkblue", alpha = 0.5) +
  geom_errorbar(aes(ymin = zL, ymax = zU), width = 0.05, alpha = 0.15,
                color = "skyblue") +
  geom_abline(slope = 1, intercept = 0, color = "red") +
  xlab("True z") + ylab("Stacked posterior of z") + theme_bw() +
  theme(panel.background = element_blank(), 
        panel.grid = element_blank(), aspect.ratio = 1)
plotz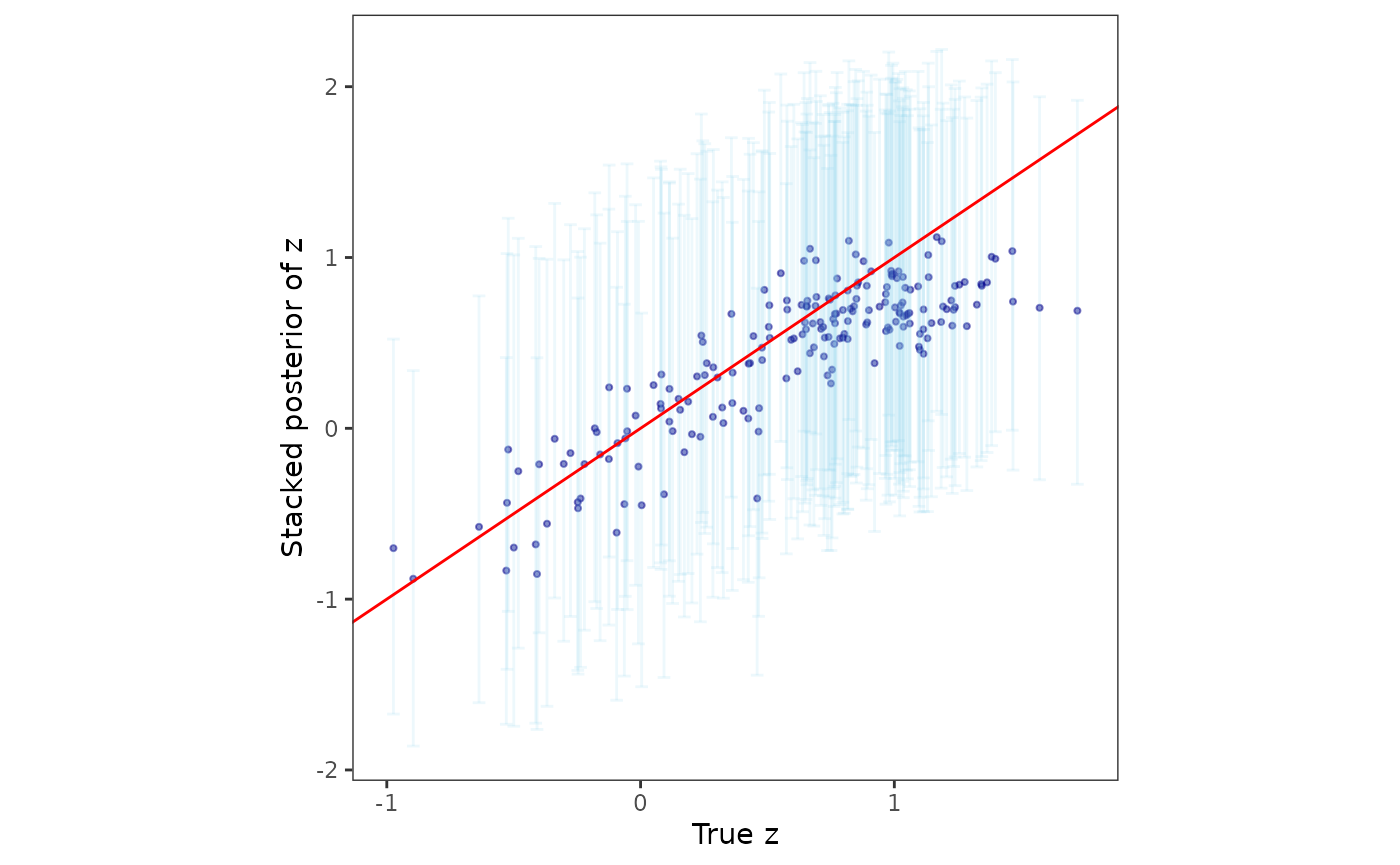

Comparison of stacked posterior with the true values

The package also provides helper functions to plot interpolated spatial surfaces in order for visualization purposes. The function surfaceplot() creates a single spatial surface plot, while surfaceplot2() creates two side-by-side surface plots. We are using the later to visually inspect the interpolated spatial surfaces of the true spatial effects and their posterior medians.

postmedian_z <- apply(post_z, 1, median)
dat$z_hat <- postmedian_z
plot_z <- surfaceplot2(dat, coords_name = c("s1", "s2"),
                       var1_name = "z_true", var2_name = "z_hat")
library(ggpubr)
ggarrange(plotlist = plot_z, common.legend = TRUE, legend = "right")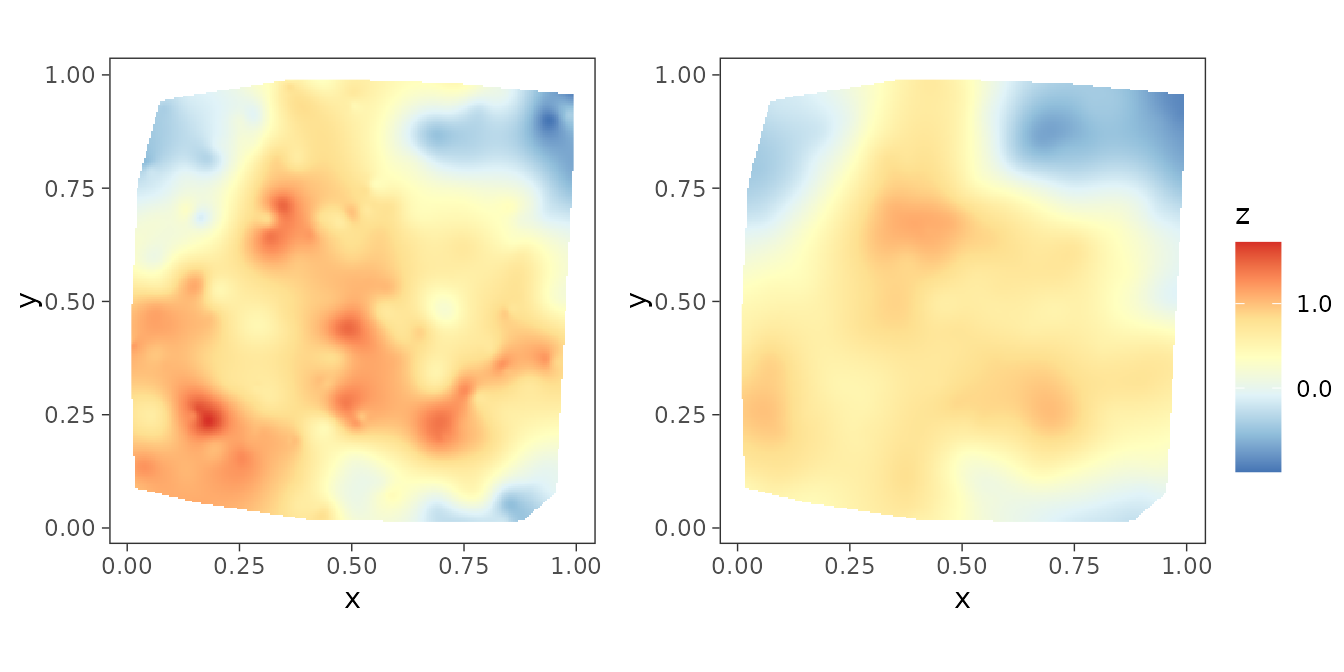

Comparison of the interploated spatial surfaces of the true random effects and the posterior medians.

Analysis of spatial non-Gaussian data

We also offer functions for Bayesian analysis of spatially point-referenced Poisson, binomial count, and binary data.

Spatial Poisson count data

We first load and plot the point-referenced Poisson count data.

data("simPoisson")
dat <- simPoisson[1:200, ] # work with first 200 observations

ggplot(dat, aes(x = s1, y = s2)) +
  geom_point(aes(color = y), alpha = 0.75) +
  scale_color_distiller(palette = "RdYlGn", direction = -1,
                        label = function(x) sprintf("%.0f", x)) +
  guides(alpha = 'none') + theme_bw() +
  theme(axis.ticks = element_line(linewidth = 0.25),
        panel.background = element_blank(), panel.grid = element_blank(),
        legend.title = element_text(size = 10, hjust = 0.25),
        legend.box.just = "center", aspect.ratio = 1)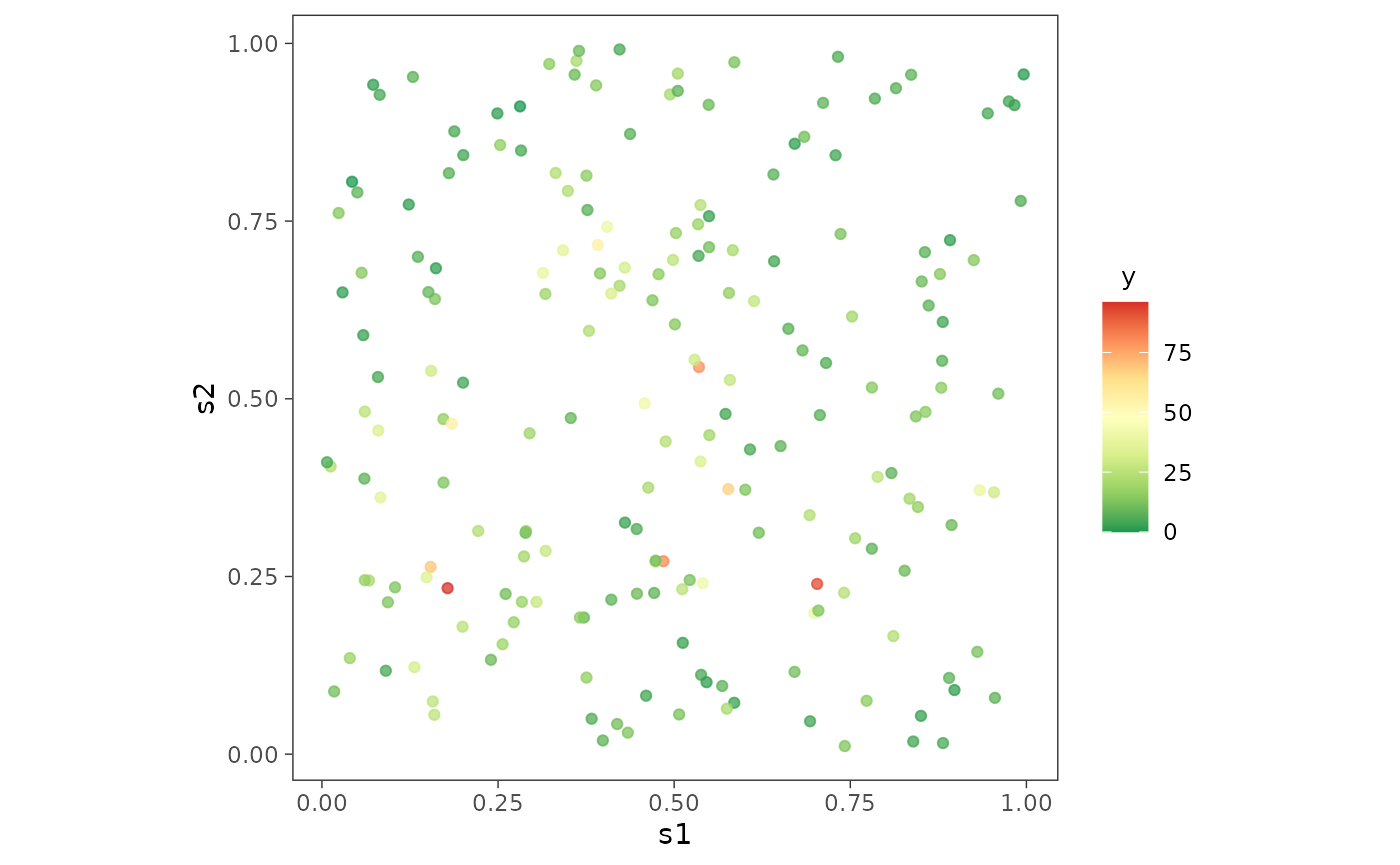

Under fixed hyperparameters

Next, we demonstrate the function spGLMexact() which delivers posterior samples of the fixed effects and the spatial random effects. The option family must be specified correctly while using this function. For instance, in the following example, the formula y ~ x1 and family = "poisson" corresponds to the spatial regression model y(s)∼𝖯𝗈𝗂𝗌𝗌𝗈𝗇(λ(s)),logλ(s)=β0+β1x1(s)+z(s).y(s) \sim \mathsf{Poisson} (\lambda(s)), \quad \log \lambda(s) = \beta_0 + \beta_1 x_1(s) + z(s)\;.

We provide fixed values of the spatial process parameters and a boundary adjustment parameter, given by the argument boundary, which if not supplied, defaults to 0.5. For details on the priors and its default value, see function documentation.

mod1 <- spGLMexact(y ~ x1, data = dat, family = "poisson",
                   coords = as.matrix(dat[, c("s1", "s2")]), cor.fn = "matern",
                   spParams = list(phi = phi0, nu = nu0),
                   priors = list(nu.beta = 5, nu.z = 5),
                   boundary = 0.5,
                   n.samples = 1000, verbose = TRUE)
#> Some priors were not supplied. Using defaults.
#> ----------------------------------------
#>  Model description
#> ----------------------------------------
#> Model fit with 200 observations.
#> 
#> Family = poisson.
#> 
#> Number of covariates 2 (including intercept).
#> 
#> Using the matern spatial correlation function.
#> 
#> Priors:
#>  beta: Gaussian
#>  mu: 0.00    0.00    
#>  cov:
#>   100.00  0.00   
#>   0.00    100.00 
#> 
#>  sigmaSq.beta ~ IG(nu.beta/2, nu.beta/2)
#>  sigmaSq.z ~ IG(nu.z/2, nu.z/2)
#>  nu.beta = 5.00, nu.z = 5.00.
#>  sigmaSq.xi = 0.10.
#>  Boundary adjustment parameter = 0.50.
#> 
#> Spatial process parameters:
#>  phi = 3.00, and, nu = 0.50.
#> 
#> Number of posterior samples = 1000.
#> ----------------------------------------

We next collect the samples of the fixed effects and summarize them. The true value of the fixed effects with which the data was simulated is β=(2,−0.5)\beta = (2, -0.5) (for more details, see the documentation of the data simPoisson).

post_beta <- mod1$samples$beta
summary_beta <- t(apply(post_beta, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
rownames(summary_beta) <- mod1$X.names
print(summary_beta)
#>                   2.5%        50%      97.5%
#> (Intercept)  0.7922293  2.0457547  3.1933523
#> x1          -0.6452358 -0.5501015 -0.4520658

Posterior recovery of scale parameters

The analytic tractability of the posterior distribution under the 𝖦𝖢𝖬\mathsf{GCM} framework is enabled by marginalizing out the scale parameters σβ2\sigma^2_\beta and σz2\sigma^2_z associated with the fixed effects β\beta and the spatial random effects zz, respectively. However, posterior samples of σβ2\sigma^2_\beta and σz2\sigma^2_z can be recovered using the function recoverGLMscale().

mod1 <- recoverGLMscale(mod1)

We visualize the posterior distributions of σβ\sigma_\beta and σz\sigma_z through histograms.

post_scale_df <- data.frame(value = sqrt(c(mod1$samples$sigmasq.beta, mod1$samples$sigmasq.z)),
                            group = factor(rep(c("sigma.beta", "sigma.z"), 
                                    each = length(mod1$samples$sigmasq.beta))))
ggplot(post_scale_df, aes(x = value)) +
  geom_density(fill = "lightblue", alpha = 0.6) +
  facet_wrap(~ group, scales = "free") + labs(x = "", y = "Density") +
  theme_bw() + theme(panel.background = element_blank(), 
                     panel.grid = element_blank(), aspect.ratio = 1)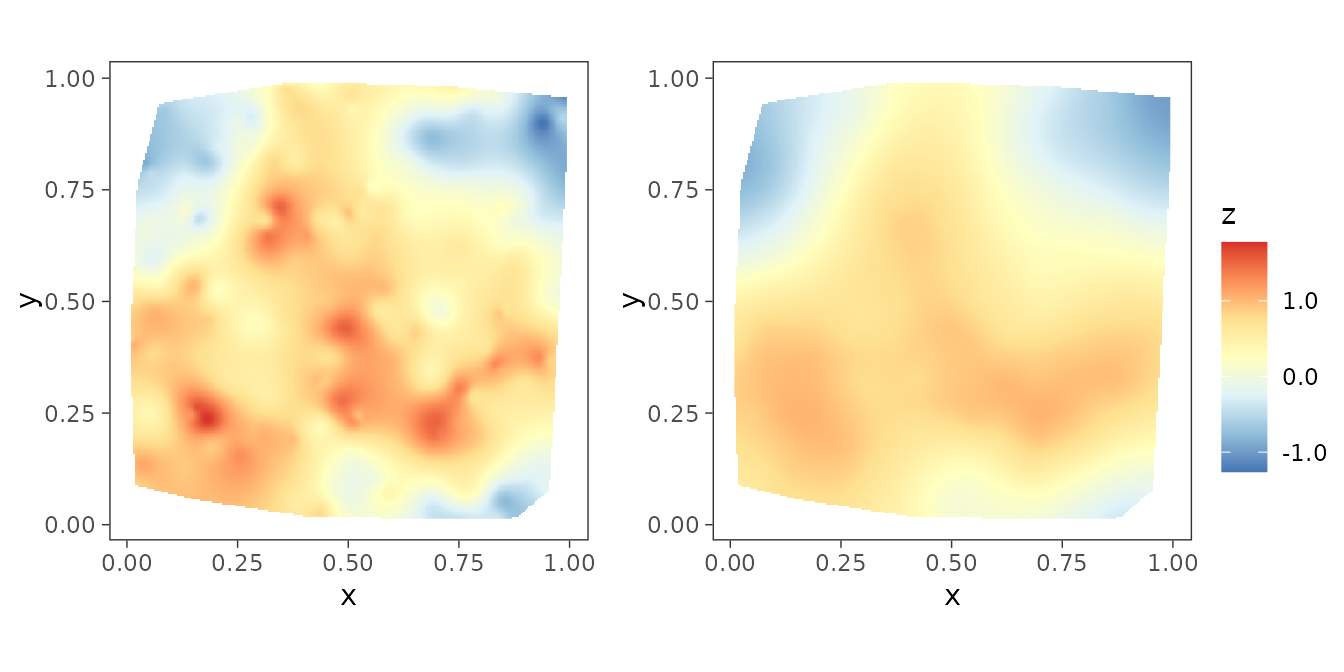

Posterior distributions of the scale parameters of the fixed and the random effects.

Using predictive stacking

Next, we move on to the function spGLMstack() that will implement our proposed stacking algorithm. The argument loopd.controls is used to provide details on what algorithm to be used to find LOO-PD. Valid options for the tag method is "exact" and "CV". We use KK-fold cross-validation by assigning method = "CV"and CV.K = 10. The tag nMC decides the number of Monte Carlo samples to be used to find the LOO-PD.

mod2 <- spGLMstack(y ~ x1, data = dat, family = "poisson",
                   coords = as.matrix(dat[, c("s1", "s2")]), cor.fn = "matern",
                   params.list = list(phi = c(3, 7, 10), nu = c(0.5, 1.5),
                                      boundary = c(0.5, 0.6)),
                   n.samples = 1000, priors = list(mu.beta = 5, nu.z = 5),
                   loopd.controls = list(method = "CV", CV.K = 10, nMC = 1000),
                   parallel = TRUE, solver = "ECOS", verbose = TRUE)
#> Some priors were not supplied. Using defaults.
#> 
#> STACKING WEIGHTS:
#> 
#>            | phi | nu  | boundary | weight |
#> +----------+-----+-----+----------+--------+
#> | Model 1  |    3|  0.5|       0.5| 0.000  |
#> | Model 2  |    7|  0.5|       0.5| 0.000  |
#> | Model 3  |   10|  0.5|       0.5| 0.000  |
#> | Model 4  |    3|  1.5|       0.5| 0.000  |
#> | Model 5  |    7|  1.5|       0.5| 0.000  |
#> | Model 6  |   10|  1.5|       0.5| 0.000  |
#> | Model 7  |    3|  0.5|       0.6| 0.000  |
#> | Model 8  |    7|  0.5|       0.6| 0.000  |
#> | Model 9  |   10|  0.5|       0.6| 0.000  |
#> | Model 10 |    3|  1.5|       0.6| 0.005  |
#> | Model 11 |    7|  1.5|       0.6| 0.724  |
#> | Model 12 |   10|  1.5|       0.6| 0.272  |
#> +----------+-----+-----+----------+--------+

We can extract information on solver status and runtime by the following.

print(mod2$solver.status)
#> [1] "optimal"
print(mod2$run.time)
#>    user  system elapsed 
#>  23.633  35.425  14.966

Further, we can recover the posterior samples of the scale parameters by passing the output obtained by running spGLMstack() once again through recoverGLMscale().

mod2 <- recoverGLMscale(mod2)

Sampling from stacked posterior

We first obtain final posterior samples by sampling from the stacked sampler.

post_samps <- stackedSampler(mod2)

Subsequently, we summarize the posterior samples of the fixed effects.

post_beta <- post_samps$beta
summary_beta <- t(apply(post_beta, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
rownames(summary_beta) <- mod3$X.names
print(summary_beta)
#>                   2.5%        50%     97.5%
#> (Intercept)  1.0880659  2.1012781  2.980541
#> x1          -0.6200398 -0.5448897 -0.477557

The synthetic data simPoisson was simulated using β=(2,−0.5)⊤\beta = (2, -0.5)^{ \scriptstyle \top }.

post_beta_df <- as.data.frame(post_beta)
post_beta_df <- post_beta_df %>%
  mutate(row = paste0("beta", row_number()-1)) %>%
  pivot_longer(-row, names_to = "sample", values_to = "value")

# True values of beta0 and beta1
truth <- data.frame(row = c("beta0", "beta1"), true_value = c(2, -0.5))

ggplot(post_beta_df, aes(x = value)) +
  geom_density(fill = "lightblue", alpha = 0.6) +
  geom_vline(data = truth, aes(xintercept = true_value), 
             color = "red", linetype = "dashed", linewidth = 0.5) +
  facet_wrap(~ row, scales = "free") + labs(x = "", y = "Density") +
  theme_bw() + theme(panel.background = element_blank(), 
                     panel.grid = element_blank(), aspect.ratio = 1)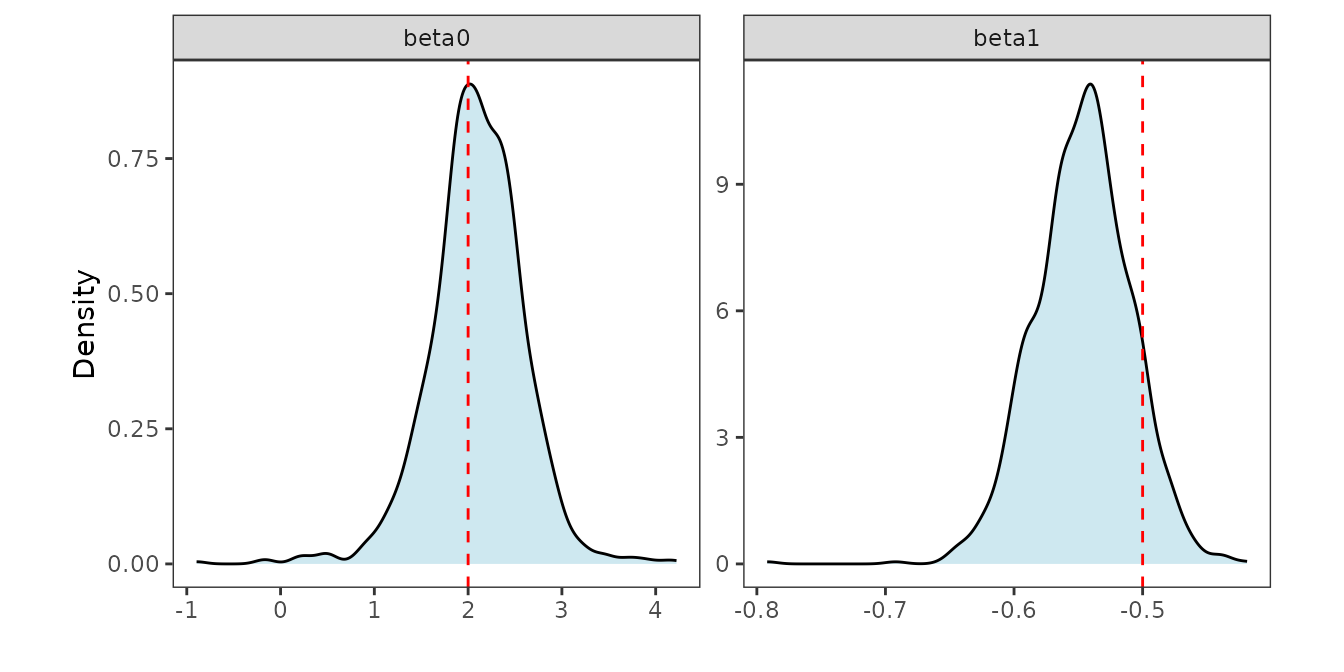

Posterior distributions of the fixed effects

Finally, we analyze the posterior samples of the spatial random effects.

post_z <- post_samps$z
post_z_summ <- t(apply(post_z, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
z_combn <- data.frame(z = dat$z_true, zL = post_z_summ[, 1],
                      zM = post_z_summ[, 2], zU = post_z_summ[, 3])

plotz <- ggplot(data = z_combn, aes(x = z)) +
  geom_point(aes(y = zM), size = 0.75, color = "darkblue", alpha = 0.5) +
  geom_errorbar(aes(ymin = zL, ymax = zU), width = 0.05, alpha = 0.15,
                color = "skyblue") +
  geom_abline(slope = 1, intercept = 0, color = "red") +
  xlab("True z") + ylab("Stacked posterior of z") + theme_bw() +
  theme(panel.background = element_blank(), 
        panel.grid = element_blank(), aspect.ratio = 1)
plotz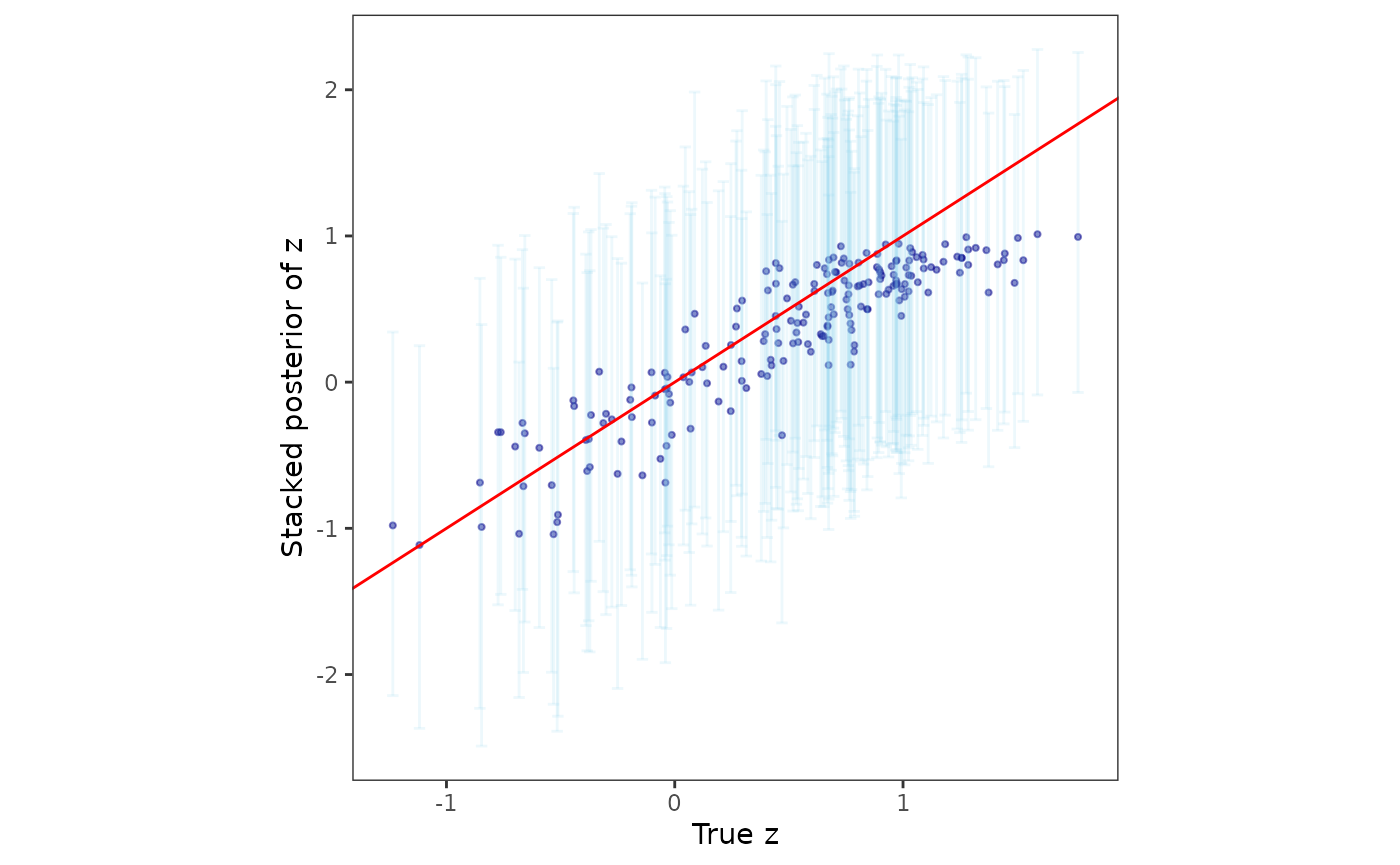

We can also compare the interpolated spatial surfaces of the true spatial effects with that of their posterior median.

postmedian_z <- apply(post_z, 1, median)
dat$z_hat <- postmedian_z
plot_z <- surfaceplot2(dat, coords_name = c("s1", "s2"),
                       var1_name = "z_true", var2_name = "z_hat")
library(ggpubr)
ggarrange(plotlist = plot_z, common.legend = TRUE, legend = "right")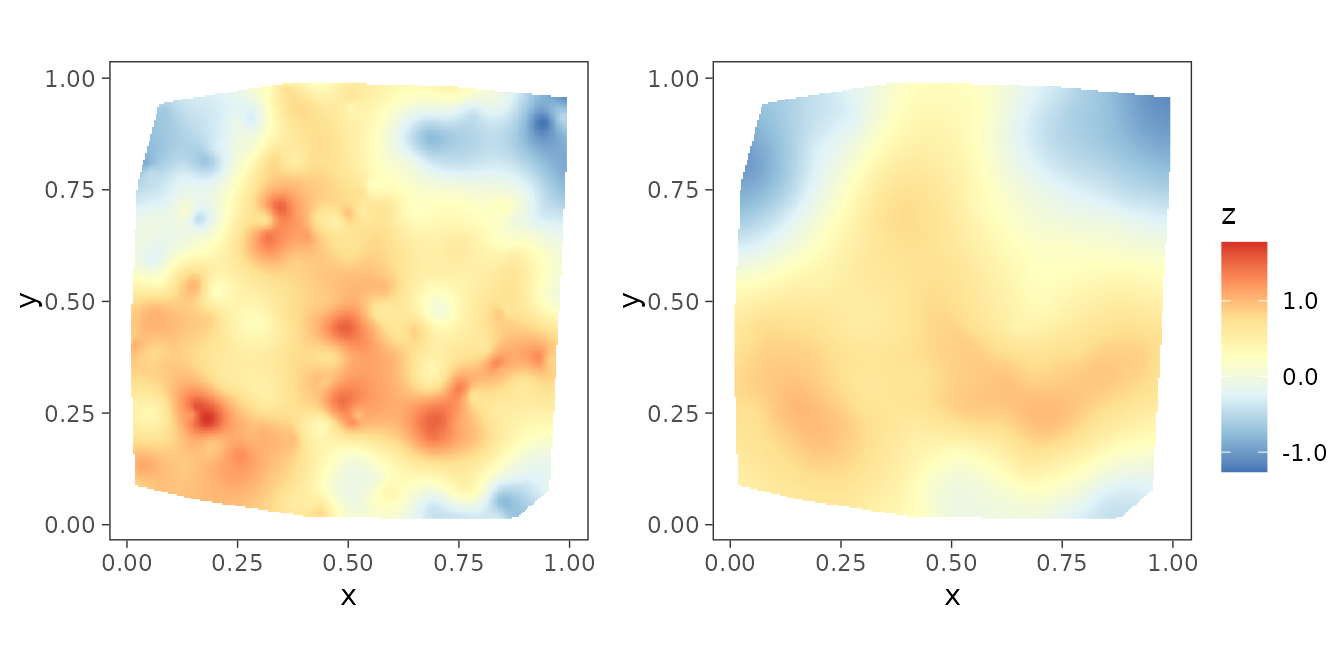

Spatial binomial count data

This will follow the same workflow as Poisson data with the exception that the structure of formula that defines the model will also contain the total number of trials at each location. Here, we present only the spGLMexact() function for brevity.

data("simBinom")
dat <- simBinom[1:200, ] # work with first 200 rows

mod1 <- spGLMexact(cbind(y, n_trials) ~ x1, data = dat, family = "binomial",
                   coords = as.matrix(dat[, c("s1", "s2")]), cor.fn = "matern",
                   spParams = list(phi = 3, nu = 0.5),
                   boundary = 0.5, n.samples = 1000, verbose = FALSE)

Similarly, we collect the posterior samples of the fixed effects and summarize them. The true value of the fixed effects with which the data was simulated is β=(0.5,−0.5)\beta = (0.5, -0.5).

post_beta <- mod1$samples$beta
summary_beta <- t(apply(post_beta, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
rownames(summary_beta) <- mod1$X.names
print(summary_beta)
#>                   2.5%        50%     97.5%
#> (Intercept) -1.1870121  0.7411895  2.738189
#> x1          -0.5852474 -0.4049237 -0.230766

Spatial binary data

Finally, we present only the spGLMexact() function for spatial binary data to avoid repetition. In this case, unlike the binomial model, almost nothing changes from that of in the case of spatial Poisson data.

data("simBinary")
dat <- simBinary[1:200, ]

mod1 <- spGLMexact(y ~ x1, data = dat, family = "binary",
                   coords = as.matrix(dat[, c("s1", "s2")]), cor.fn = "matern",
                   spParams = list(phi = 4, nu = 0.4),
                   boundary = 0.5, n.samples = 1000, verbose = FALSE)

Similarly, we collect the posterior samples of the fixed effects and summarize them. The true value of the fixed effects with which the data was simulated is β=(0.5,−0.5)\beta = (0.5, -0.5).

post_beta <- mod1$samples$beta
summary_beta <- t(apply(post_beta, 1, function(x) quantile(x, c(0.025, 0.5, 0.975))))
rownames(summary_beta) <- mod1$X.names
print(summary_beta)
#>                   2.5%        50%      97.5%
#> (Intercept) -1.2015085  0.3212393 2.20401790
#> x1          -0.6653012 -0.3229634 0.07179601

References

Vehtari, Aki, Andrew Gelman, and Jonah Gabry. 2017. “Practical Bayesian Model Evaluation Using Leave-One-Out Cross-Validation and WAIC.” Statistics and Computing 27 (5): 1413–32. https://doi.org/10.1007/s11222-016-9696-4.